2.8 效率

INFO

译者：laziyu

对应：无

选择如何表示和处理数据时，常要权衡效率。效率指计算所用的资源，例如求函数结果或表示对象所需的时间与内存，这些数量会因实现细节而差异巨大。

2.8.1 测量效率

精确测量运行时间或内存很难，因为结果取决于机器配置等诸多细节。更可靠的方式是统计某些事件发生的次数，例如函数调用次数。

回到第一个树递归函数 fib。

>>> def fib(n):
        if n == 0:
            return 0
        elif n == 1:
            return 1
        else:
            return fib(n - 2) + fib(n - 1)
>>> fib(5)
5

计算 fib(6) 的模式如图：为求 fib(5) 需要 fib(3) 与 fib(4)，求 fib(3) 又需 fib(1) 与 fib(2)。整体演化像一棵树，遍历时每个蓝点表示某个斐波那契数完成计算。

fib

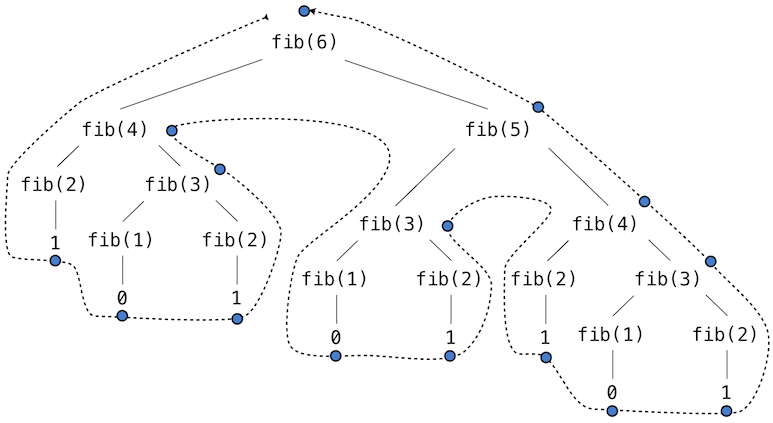
它很有教学意义，但计算斐波那契数极其低效，存在大量冗余：fib(3) 的整个过程会被重复。

我们可以测量这种低效。高阶函数 count 返回与参数等效的函数，并维护 call_count 属性，用以统计调用次数。

>>> def count(f):
        def counted(n):
            counted.call_count += 1
            return f(n)
        counted.call_count = 0
        return counted

统计调用次数可见其增长比斐波那契数列本身还快，这是树递归的典型特征。

>>> fib = count(fib)
>>> fib(19)
4181
>>> fib.call_count
10946

空间。要了解函数的空间需求，需要说明环境模型如何使用、保留和回收内存。计算表达式时，解释器保存所有活动环境及其引用的值和帧。环境为某个表达式提供求值上下文即为活动；当创建其首帧的调用返回时，环境变为非活动。

例如计算 fib 时，解释器按树结构顺序计算各值。它只需跟踪当前节点之上的节点，其他分支所用内存可回收，因为不再影响未来计算。树递归所需空间与树的最大深度成正比。

以下的图表描述了计算 fib(3) 时所创建的环境。在计算初始应用 fib 的返回表达式时，表达式 fib(n-2) 被计算，得到一个值为 0。一旦这个值被计算出来，相应的环境帧（被标记为灰色）就不再需要：它不是一个活动环境的一部分。因此，一个良好设计的解释器可以回收用于存储该帧的内存。另一方面，如果解释器当前正在计算 fib(n-1) ，则通过这个 fib 应用（其中 n 为 2）所创建的环境是活动的。反过来，最初用于将 fib 应用于 3 的环境是活动的，因为其返回值尚未被计算出来。

高阶函数 count_frames 用于跟踪未返回的调用次数 open_count，记录计算过程中活动调用数。max_count 是 open_count 曾达到的最大值，对应同时活动的最大帧数。

>>> def count_frames(f):
        def counted(n):
            counted.open_count += 1
            counted.max_count = max(counted.max_count, counted.open_count)
            result = f(n)
            counted.open_count -= 1
            return result
        counted.open_count = 0
        counted.max_count = 0
        return counted
>>> fib = count_frames(fib)
>>> fib(19)
4181
>>> fib.open_count
0
>>> fib.max_count
19
>>> fib(24)
46368
>>> fib.max_count
24

总结：fib 的空间需求（按活动帧数）比输入小 1，通常较小；而按递归调用次数衡量的时间需求比输出大，通常巨大。

2.8.2 记忆化

树递归通常可用**记忆化（memoization）**提效：函数会保存已见参数的返回值，第二次调用如 fib(25) 就直接返回缓存。

记忆化可自然写成高阶函数或装饰器。下面创建缓存（cache）存储已计算结果，索引为参数；用字典做缓存要求参数不可变。

>>> def memo(f):
        cache = {}
        def memorized(n):
            if n not in cache:
                cache[n] = f(n)
            return cache[n]
        return memorized

如果我们将 memo 应用于斐波那契数列的递归计算，将会产生一个新的计算模式，如下所示。

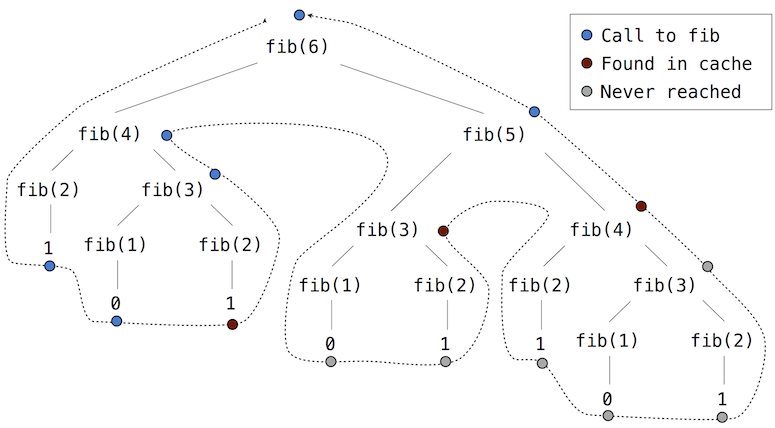
fib_memo

在计算 fib(5) 时，在计算右侧分支的 fib(4) 时，已经计算过的 fib(2) 和 fib(3) 的结果被重复使用。因此，许多树递归计算根本不需要进行。

通过使用 count 函数，我们可以看到对于每个唯一的输入，fib 函数实际上只被调用一次。

>>> counted_fib = count(fib)
>>> fib =memo(count_fib)
>>> fib(19)
4181
>>> counted_fib.call_count
20
>>> fib(34)
5702887
>>> counted_fib.call_count
35

2.8.3 增长阶数

计算过程消耗资源的速率差异巨大，前面的例子已显示这一点。准确估计调用使用的空间或时间很难，取决于诸多因素。一个有用的分析方法是按需求相似的过程分类，常用分类是增长阶（orders of growth），用简单术语描述资源需求随输入的增长。

为介绍增长阶，分析函数 count_factors：它计算能整除输入 $n$ 的整数个数，尝试用每个不超过平方根的整数去除 $n$ 。实现利用了：若 $k$ 整除 $n$ 且 $k < \sqrt{n}$ ，必有另一因子 $j = n / k$ ，且 $j > \sqrt{n}$ 。

计算 count_factors 需要多少时间？精确答案因机器而异，但可以做一些普遍观察：while 执行次数是小于等于 $\sqrt{n}$ 的最大整数；while 前后的语句各执行一次。总执行语句数约为 $w * \sqrt{n} + v$ ，其中 $w 是循环体语句数，v` 是循环外语句数。虽然不精确，但足以描述时间随输入的函数关系。

更精确的描述很难。 $w$ 与 $v$ 并非恒定，因为因子相关赋值有时执行、有时不执行。增长阶分析让我们忽略这些细节，关注整体趋势。特别地，count_factors 的增长阶表明其时间以 $\sqrt{n}$ 级别增长，允许常数因子的误差。

Theta 符号（Theta notation） 用于表示算法的渐进性能。设参数 $n$ 衡量输入规模，用 $R (n)$ 表示对规模 $n$ 所需的资源量。在前例中， $n$ 是要求值的数字，亦可有其他定义，例如把 $n$ 视为平方根近似的有效位数。

$R (n)$ 可表示内存用量、基本步骤数等。在每步耗时固定的机器上，计算时间与执行的基本步骤数成正比。

若存在与 $n$ 无关的正常数 $k_{1}$ 、 $k_{2}$ ，使得对所有大于某最小值 $m$ 的 $n$ 满足

k_{1} \cdot f (n) \leq R (n) \leq k_{2} \cdot f (n)

则称 $R (n)$ 的增长阶为 $Θ (f (n))$ ，记作 $R (n) = Θ (f (n))$ （读作 “theta of f(n)”）。也就是说，对大 $n$ ， $R (n)$ 夹在与 $f (n)$ 成比例的上下界之间：

下界 $k_{1} \cdot f (n)$
上界 $k_{2} \cdot f (n)$

检查函数体可用此定义展示 count_factors(n) 的步骤数量以 $Θ (\sqrt{n})$ 增长。

下界：取 $k_{1} = 1$ 、 $m = 0$ ，对任意 $n > 0$ ，count_factors(n) 至少需 $1 \cdot \sqrt{n}$ 步。while 外至少执行 4 行，每行至少 1 步；while 体内至少 2 行，加上 while 头，每次至少 1 步；循环体至少执行 $\sqrt{n} - 1$ 次。合计至少 $4 + 3 \cdot (\sqrt{n} - 1)$ 步，始终大于 $k_{1} \cdot \sqrt{n}$ 。

上界：假设函数体任一行至多需 $p$ 步（此处成立）。则 count_factors(n) 最多需 $p \cdot (5 + 4 \sqrt{n})$ 步：while 外 5 行，循环内 4 行（含 while 头），即便每个 if 都为真，上界仍成立。取 $k_{2} = 5 p$ ，所需步骤始终小于 $k_{2} \cdot \sqrt{n}$ 。证明完成。

2.8.4 示例：指数运算

考虑计算给定数的指数问题。我们希望有一个函数，它以底数 $b$ 和正整数指数 $n$ 作为参数，并计算 $b_{n}$ 。一种实现方法是通过递归定义：

b^{n} = b \cdot b^{(n - 1)}

b^{0} = 1

这个递归定义可以很容易的转化为递归函数：

>>> def exp(b, n):
        if n == 0:
            return 1
        return b * exp(b, n - 1)

这是一个线性递归过程，它需要 $Θ (n)$ 步骤和 $Θ (n)$ 空间。就像阶乘一样，我们可以很容易地设计一个等效的线性迭代版本，它需要相似数量的步骤，但只需要常量空间。

这意味着递归的指数计算是一个线性过程，它的时间和空间复杂度都随着指数 $n$ 的增长而线性增加。与此相反，通过线性迭代，我们可以将计算复杂度优化为仅需常数级的空间，但步骤数量仍然是与指数 $n$ 成线性关系的。

>>> def exp_iter(b, n):
        result = 1
        for _ in range(n):
            result = result * b
        return result

我们可以通过使用连续平方法来以更少的步骤计算指数。例如，计算 b 的 8 次幂可以如下进行：

b^{8} = b * (b * (b * (b * (b * (b * (b * b))))))

而我们可以使用三次乘法来计算它：

b^{2} = b * b

b^{4} = b^{2} * b^{2}

b^{8} = b^{4} * b^{4}

这种方法对于指数是 2 的幂次的情况非常有效。我们也可以利用连续平方法来计算一般情况下的指数，如果我们使用如下递归规则：

b^{n} = {\begin{cases} {(b^{\frac{n}{2}})}^{2} & 如果 n 是偶数 \\ b \cdot b^{n - 1} & 如果 n 是奇数 \end{cases}

我们也可以用一个递归函数的方式来表达这个方法：

>>> def square(x):
        return x * x

>>> def fast_exp(b, n):
        if n == 0:
            return 1
        if n % 2 == 0:
            return square(fast_exp(b, n // 2))
        else:
            return b * fast_exp(b, n - 1)

>>> fast_exp(2, 100)
1267650600228229401496703205376

通过快速指数运算（fast_exp），计算过程在时间和空间上都以对数级别随 $n$ 增长。要理解这一点，观察一下使用 fast_exp 计算 $b$ 的 $2 n$ 次幂仅仅比计算 $b$ 的 $n$ 次幂多进行一次乘法。因此，我们可以看到每一次允许的新乘法使得我们能够计算的指数大小翻倍（粗略估计）。因此，对于指数 $n$ ，所需的乘法次数大致以 2 为底数的 $n$ 的对数增长。这个过程具有 $Θ (l o g_{n})$ 的增长阶。

当 $n$ 变得很大时， $Θ (l o g_{n})$ 增长阶与 $Θ (n)$ 增长阶之间的差异会变得非常明显。例如，对于 $n$ 为 1000，使用 fast_exp 只需要 14 次乘法，而不是 1000 次。这显示了使用快速指数运算相对于普通指数运算在效率上的巨大优势。

2.8.5 增长类别

增长阶是为了简化计算过程的分析和比较而设计的。许多不同的计算过程可以具有等效的增长阶，这表示它们的增长方式相似。对于计算机科学家来说，了解和识别常见的增长阶并确定具有相同增长阶的过程是一项重要的技能。

常数项：常数项不影响计算过程的增长阶。因此，例如， $Θ (n)$ 和 $Θ (500 \cdot n)$ 具有相同的增长阶。这个性质来自于 $Θ$ 符号的定义，它允许我们选择任意的常数 $k_{1}$ 和 $k_{2}$ （比如 $\frac{1}{500}$ ）作为上界和下界。为了简洁起见，增长阶中常数通常被忽略。

对数：对数的底数不影响计算过程的增长阶。例如， $l o g 2 (n)$ 和 $l o g 10 (n)$ 具有相同的增长阶。改变对数的底数等价于乘以一个常数因子。

嵌套：当内部的计算过程在外部过程的每一步中重复执行时，整个过程的增长阶是外部和内部过程的步骤数的乘积。

例如，下面的函数 overlap 计算列表 a 中与列表 b 中出现的元素数量。

>>> def overlap(a, b):
        count = 0
        for item in a:
            if item in b:
                count += 1
        return count

>>> overlap([1, 3, 2, 2, 5, 1], [5, 4 ,2])
3

对于列表的 in 运算符，其时间复杂度为 $Θ (n)$ ，其中 $n$ 是列表 b 的长度。它被应用 $Θ (m)$ 次，其中 $m$ 是列表 a 的长度。表达式 item in b 是内部过程，而 for item in a 循环是外部过程。该函数的总增长阶是 $Θ (m \cdot n)$ 。

低阶项。随着计算过程的输入增长，计算中增长最快的部分将主导总的资源使用。 $Θ$ 符号捕捉了这种直觉。总的来说，除了增长最快的项外，其他项都可以忽略而不影响增长阶。

例如，考虑函数 one_more，它返回列表 a 中有多少个元素是另一个元素的值加 1。也就是说，在列表 [3, 14, 15, 9] 中，元素 15 比 14 大 1，所以 one_more 将返回 1。

>>> def one_more(a):
        return overlap(a, [x + 1 for x in a])

>>> one_more([3, 14, 15, 9])
1

这个计算分为两个部分：列表推导和对 overlap 的调用。对于长度为 $n$ 的列表 a，列表推导需要 $Θ (n)$ 步，而对 overlap 的调用需要 $Θ (n^{2})$ 步。这两部分的总步数是 $Θ (n + n^{2})$ ，但这并不是表达增长阶最简单的方式。

$Θ (n^{2} + k * n)$ 和 $Θ (n^{2})$ 对于任意常数 $k$ 来说是等价的，因为对于任何 $k$ ， $n^{2}$ 项在足够大的 $n$ 下将主导总和。这里的边界要求仅对于大于某个最小值 $m$ 的 $n$ 成立，从而确立了这种等价性。为简洁起见，增长阶中的低阶项通常被忽略，所以我们不会在 $t h e t a$ 表达式中看到求和。

常见的类别。 通过这些等价性，我们可以得到一小组常见的类别来描述大多数计算过程。最常见的类别如下，按从最慢到最快的增长顺序列出，并描述了随着输入增加而增长的情况。接下来将给出每个类别的例子。

类别	$Θ$ 表示	增长阶描述	例子
常数	$Θ (1)$	增长与输入无关	`abs`
对数	$Θ (l o g_{n})$	增长与输入的大小成正比	`fast_exp`
线性	$Θ (n)$	随着输入的递增，计算过程所需的资源会增加 n 个单位	`exp`
乘方	$Θ (n^{2})$	随着输入的递增，计算过程所需的资源会增加 n 个单位	`one_more`
指数	$Θ (b^{n})$	随着输入的递增，计算过程所需的资源会成倍增加	`fib`

除了这些之外，还有其他的增长阶类别，例如 count_factors 的 $Θ (\sqrt{n})$ 增长。然而，上述列举的类别是特别常见的。

指数增长描述了许多不同的增长阶，因为改变底数 $b$ 会影响增长阶。例如，我们的树递归斐波那契计算 fib 的步数随输入 $n$ 呈指数增长。特别地，我们可以证明第 $n$ 个斐波那契数是最接近于

\frac{ϕ^{n - 2}}{\sqrt{5}}

的整数，其中 $ϕ$ 是黄金比例：

ϕ = \frac{1 + \sqrt{5}}{2} \approx 1.6180

我们还提到步数与结果值成正比，所以树递归过程需要 $Θ (ϕ^{n})$ 步，这是一个随着 $n$ 以指数级别增长的函数。

2.8 效率 ​

2.8.1 测量效率 ​

2.8.2 记忆化 ​

2.8.3 增长阶数 ​

2.8.4 示例：指数运算 ​

2.8.5 增长类别 ​